目录
数据的表示
进制转换
R进制转十进制使用按权展开法,每一位数都是
十进制转R进制使用短除法,将R作为除数,记录余数,逆序拼接
每三个二进制位对应一个八进制位,每四个二进制位对应一个十六进制位
编码
| 数值1 | 数值-1 | 1-1(1加负1) | |
|---|---|---|---|
| 原码 | 0000 0001 | 1000 0001 | 1000 0010 |
| 反码 | 0000 0001 | 1111 1110 | 1111 1111 |
| 补码 | 0000 0001 | 1111 1111 | 0000 0000 |
| 移码 | 1000 0001 | 0111 1111 | 1000 0000 |
正数的原码、反码、补码相等
负数的反码:符号位不变,其他位按位取反
负数的补码:反码+1
移码:对补码首位取反
表示范围:
| 整数 | |
|---|---|
| 原码 | ~ |
| 反码 | ~ |
| 补码 | ~ |
原码和反码中+0与-0的表示不同,补码中相同,所以比原码和反码的范围少1
浮点数运算
浮点数表示:,M:尾数,e:指数,R:基数
对阶→尾数计算→结果格式化
计算机结构
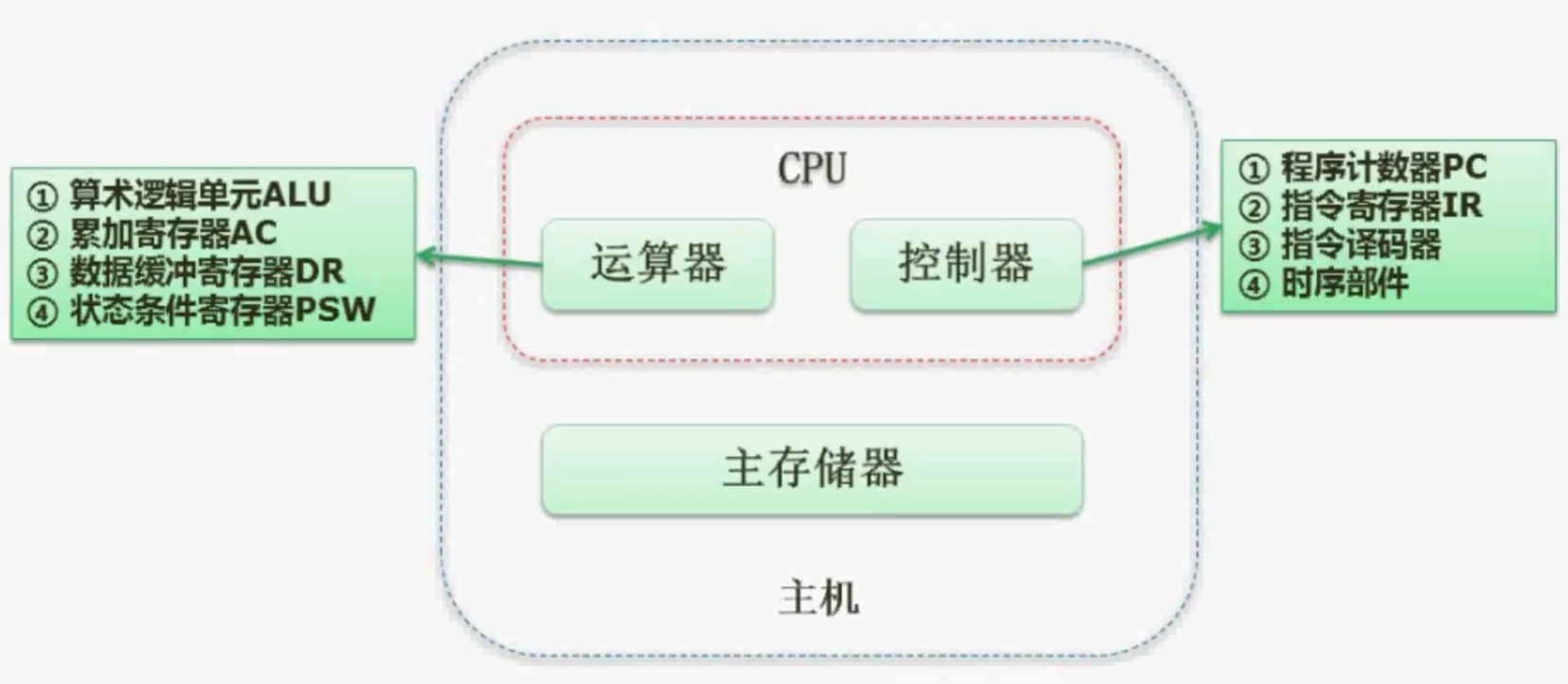
状态条件寄存器:存储运算过程中相关的标志位
Flynn分类法
分类依据:指令流和数据流
| 体系结构类型 | 结构 | 关键特性 | 代表 |
|---|---|---|---|
| 单指令流单数据流 SISD | 控制部分:一个 处理器:一个 主存模块:一个 | 单处理器系统 | |
| 单指令流多数据流 SIMD | 控制部分:一个 处理器:多个 主存模块:多个 | 各处理器以异步的形式执行同一条指令 | 并行处理机 阵列处理机(数组类型) 超级向量处理机 |
| 多指令流单数据流 MISD | 控制部分:多个 处理器:一个 主存模块:多个 | 被证明不可能,至少是不实际 | 目前没有,有文献称流水线计算机为此类 |
| 多指令流多数据流 MIMD | 控制部分:多个 处理器:多个 主存模块:多个 | 能够实现作业、任务、指令等各级全面并行 | 多处理机系统 多计算机 |
CISC与RISC
| 指令系统类型 | 指令 | 寻址方式 | 实现方式 | 其它 |
|---|---|---|---|---|
| CISC(复杂) | 数量多,使用频率差别大,可变长格式 | 支持多种 | 微程序控制技术(微码) | 研制周期长 |
| RISC(精简) | 数量少,使用频率接近,定长格式,大部分为单周期指令,操作寄存器,只有Load/Store操作内存 | 支持方式少 | 增加了通用寄存器;硬布线逻辑控制为主;适合采用流水线 | 优化编译,有效支持高级语言 |
流水线技术
几乎每次考试都会考到
概念
流水线是指在程序执行时多条指令重叠进行操作的一种准并行处理实现技术。各种部件同时处理是针对不同指令而言的,它们可同时为多条指令的不同部分进行工作,以提高各部件的利用率和指令的平均执行速度
取指→分析→执行
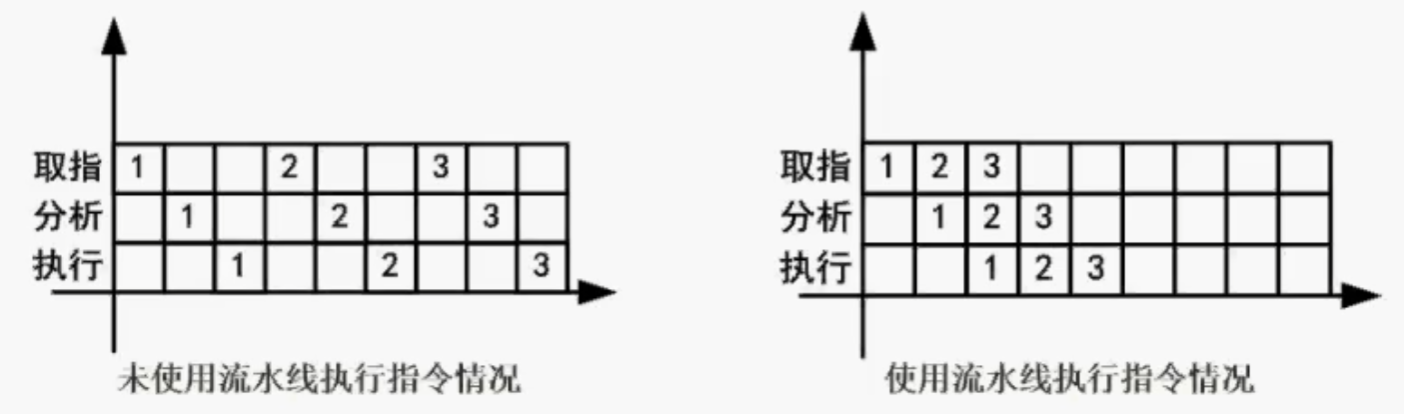
计算
流水线周期为执行时间最长的一段
流水线计算公式:1条指令执行时间 + (指令条数 - 1) * 流水线周期*
- 理论公式:
- 实践公式:
- 考试时首先用到理论公式,若无理论公式答案再用实践公式
吞吐率计算
在单位时间内流水线处理的任务数量或输出的结果数量
基本公式:
流水线最大吞吐率:
加速比计算
完成同一批任务,不使用流水线的时间与使用流水线的时间的比值
效率计算
流水线的设备利用率。在时空图上,流水线的效率定义为n个任务占用的时空区与k个流水段总的时空区之比
公式:
例
例1

- 流水线周期为2ns
- 流水线执行时间使用理论公式计算为
- 流水线执行时间使用实践公式计算为
- 流水线吞吐率
- 最大吞吐率
- 加速比
例2
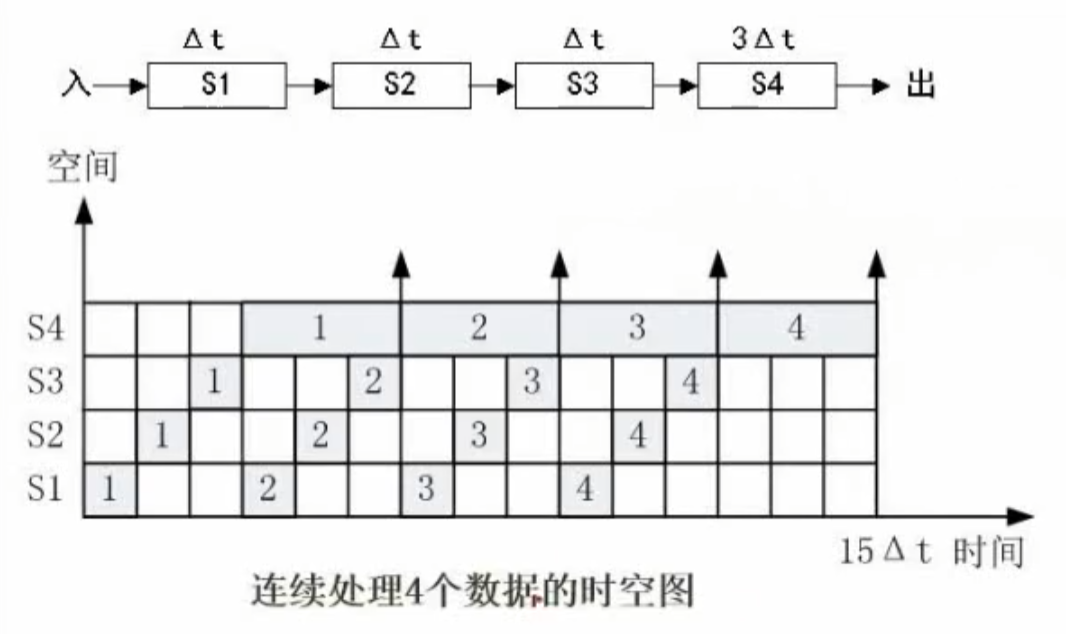
- 流水线效率
存储系统
层次化存储结构
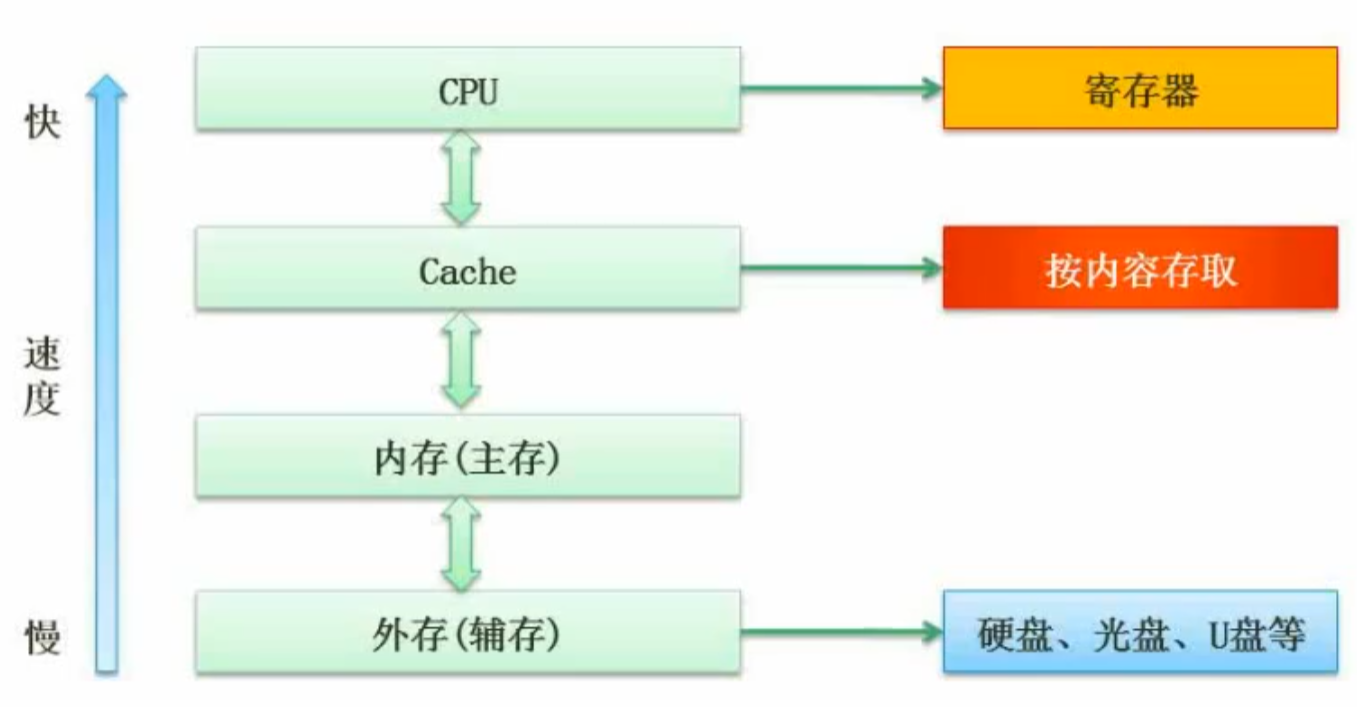
寄存器容量极小,速度极快
Cache是高速缓存,按内容存取,不是必需的,K字节和M字节
从上到下,速度减慢,容量增加
Cache
- 提高CPU数据输入输出的速率,突破冯·诺依曼瓶颈(即CPU与存储系统间数据传送带宽限制)
- 在计算机的存储系统体系中,Cache是访问速度最快的层次(有寄存器可选时选寄存器,没有寄存器选cache)
- 使用Cache改善系统性能的依据;程序的局部性原理
:Cache的周期时间(1ns),:主存储器周期时间(1ms),:以读操作为例使用“Cache+主存储器”的系统的平均周期,:访问命中率(95%),1-h:失效率(未命中率)
局部性原理
- 时间局部性:顺序执行的代码,分成不同的块,放入cache中,特别是for循环比较明显,将其运行的代码放入cache中,每次循环从cache调用即可
- 空间局部性:数组较为明显,当程序首先访问某空间,立即访问邻近的空间
- 工作集理论:工作集是进程运行时被频繁访问的页面集合
主存
分类
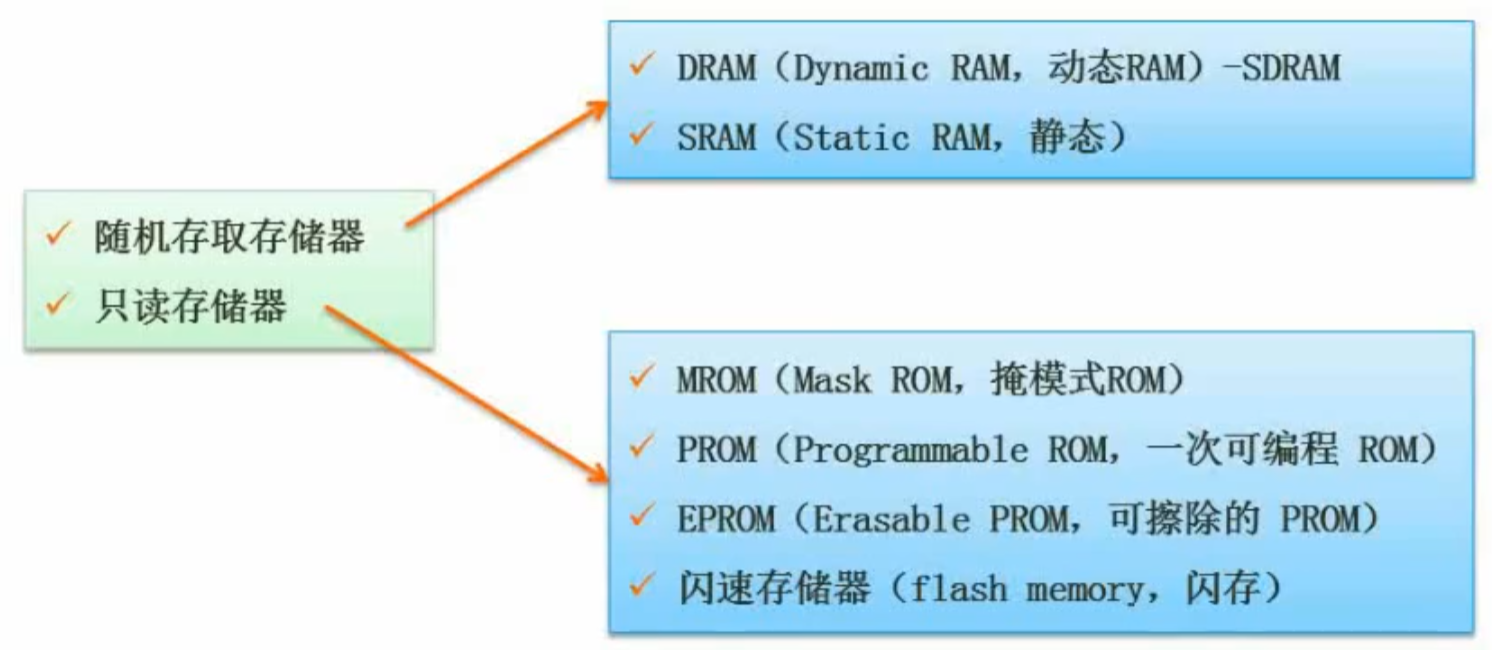
编址
把芯片组成相应的存储器
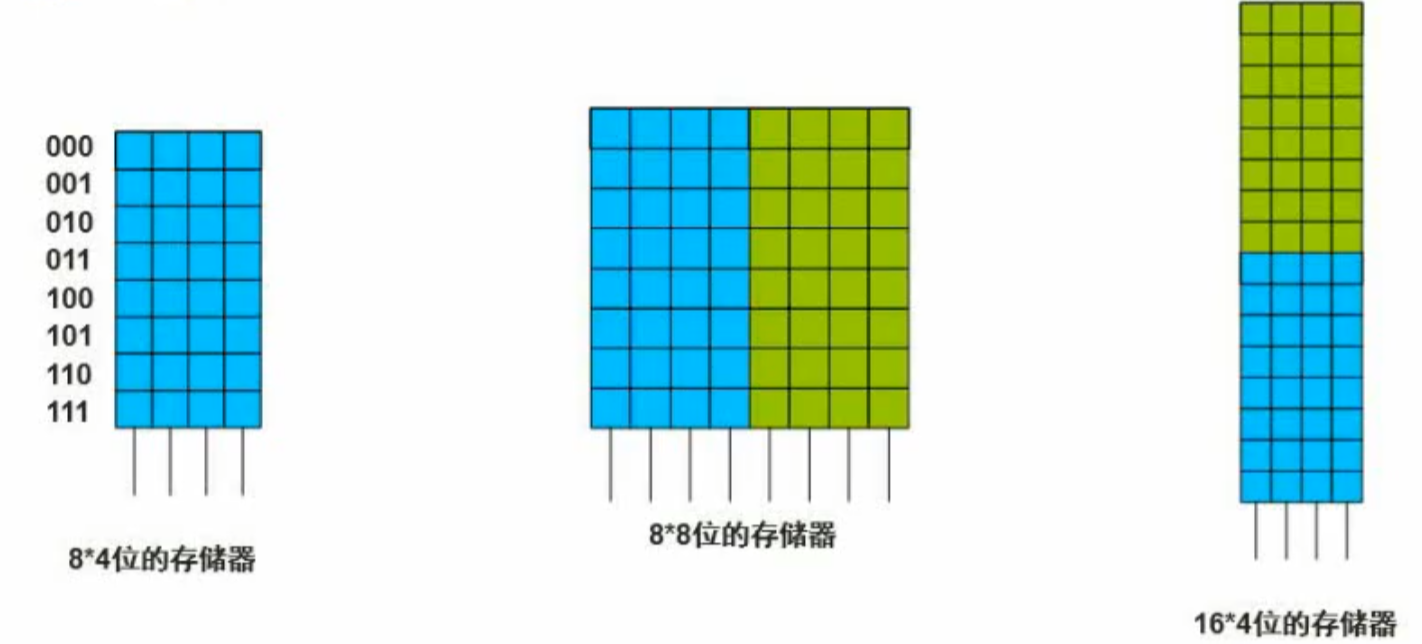
地址单元:
每个存储单元存储几位:,得出
磁盘结构与参数
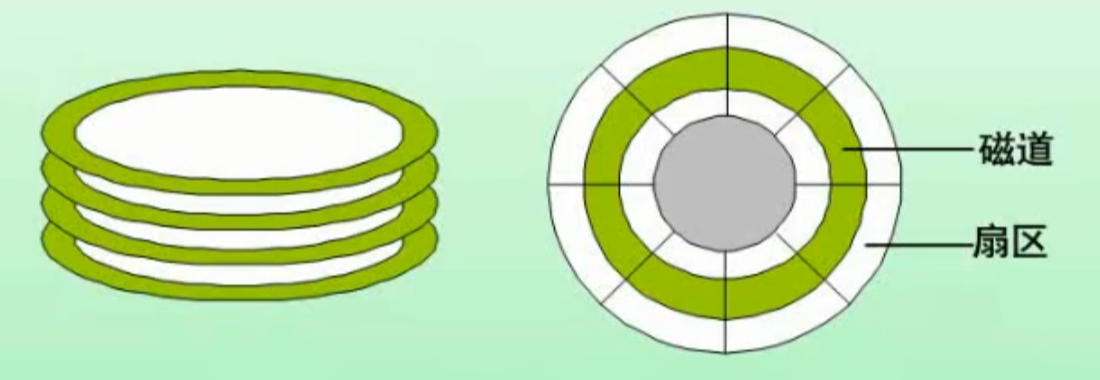
存取时间 = 寻道时间 + 等待时间(平均定位时间 + 转动延迟)
寻道时间是磁头移动到磁道所需的时间,等待时间为等待读写的扇区转到磁头下方所用的时间
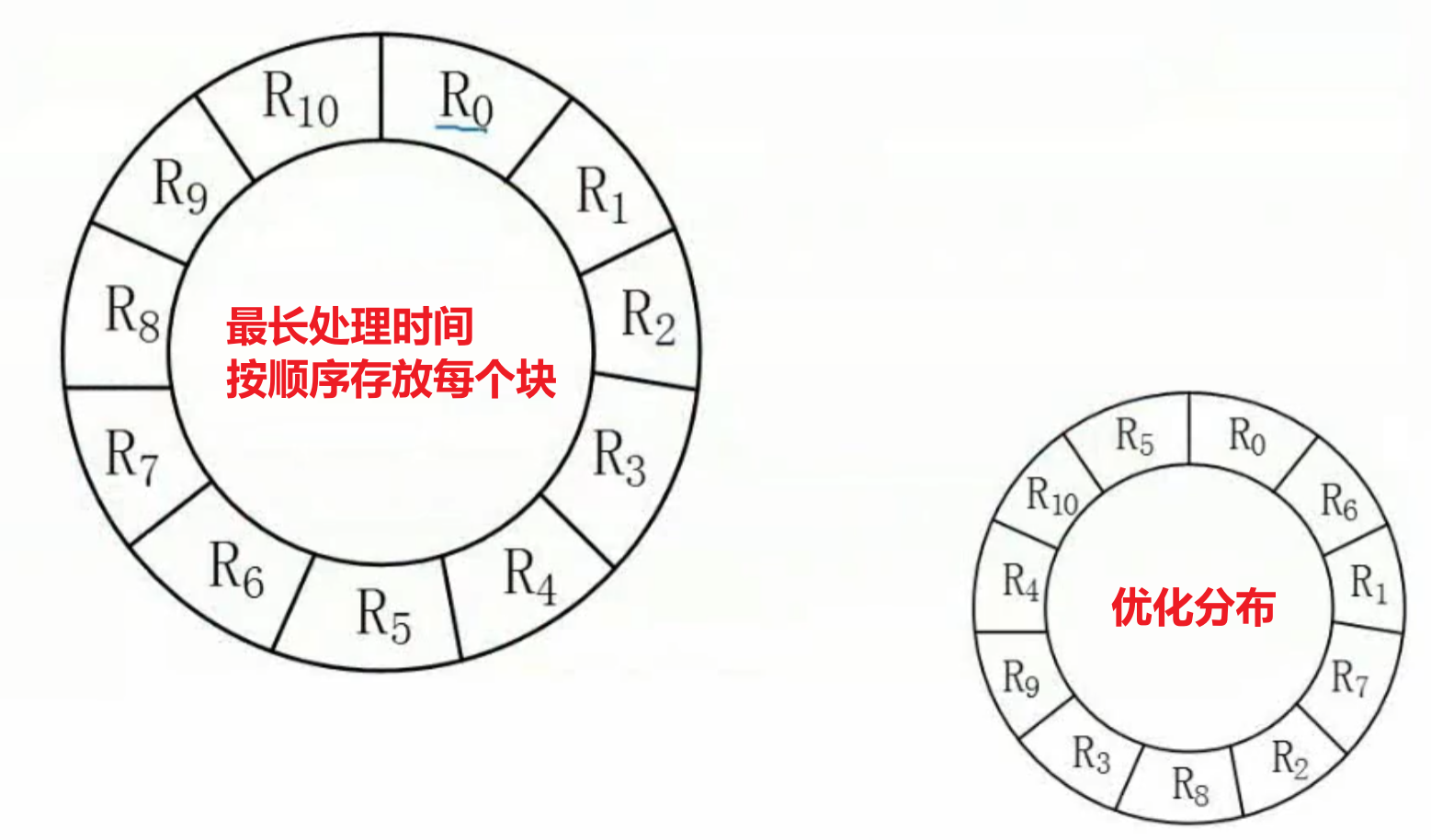
磁盘旋转周期为33ms,则平均每一个扇区的旋转时间为3ms,即读取时间为3ms
单缓冲区意味着一次只能处理一个记录,当被读取并处理时,磁盘继续转动,要想继续处理,需要等待磁盘继续旋转至磁头在处
所以最长处理时间为
对于最少处理时间,最优分布情况为,我们希望在处理完毕后,磁头恰好处于的位置,以此类推,最少处理时间为,如下图所示
总线系统
根据总线所处的位置不同通常分为三种类型:
- 内部总线:微机内部各个外围芯片与处理器之间的总线
- 系统总线:CPU、主存、I/O设备各大部件之间的信息传输线
- 数据总线
- 地址总线
- 控制总线
- 外部总线:微机和外部的总线
可靠性
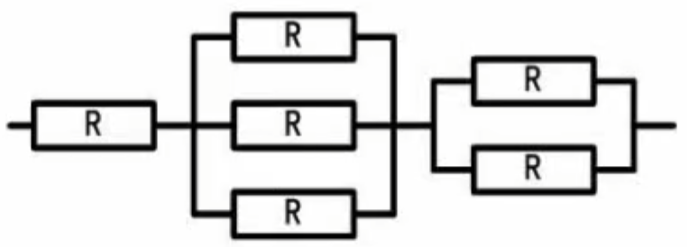
串联系统与并联系统
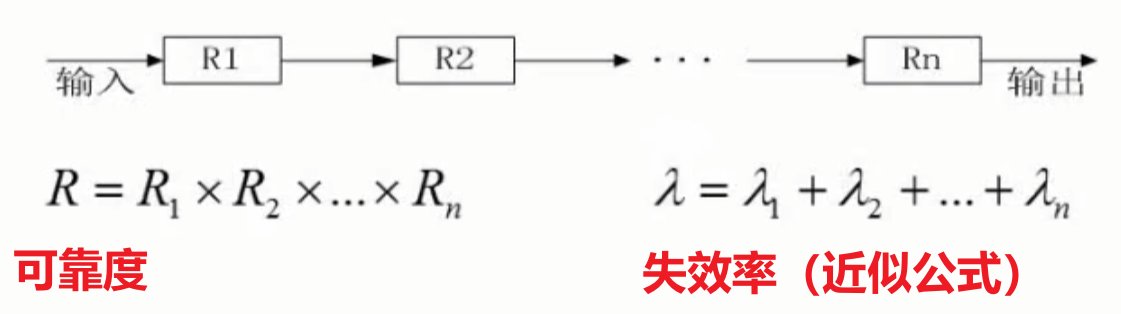
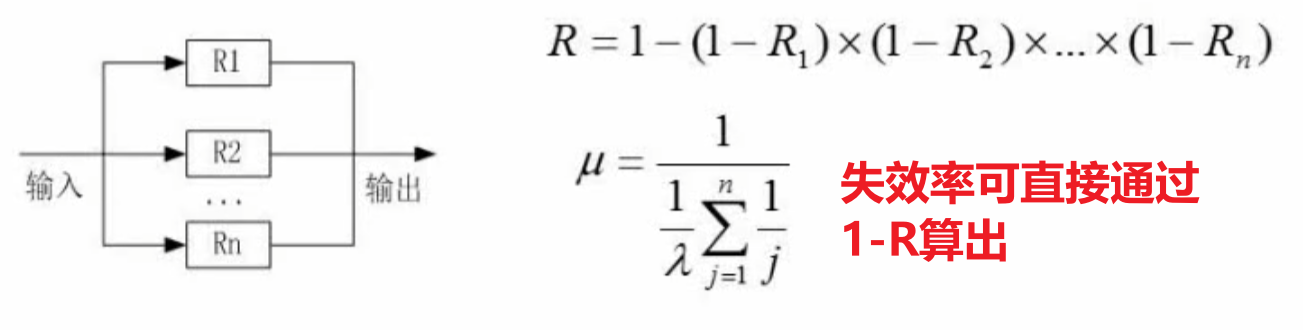
n模冗余模型
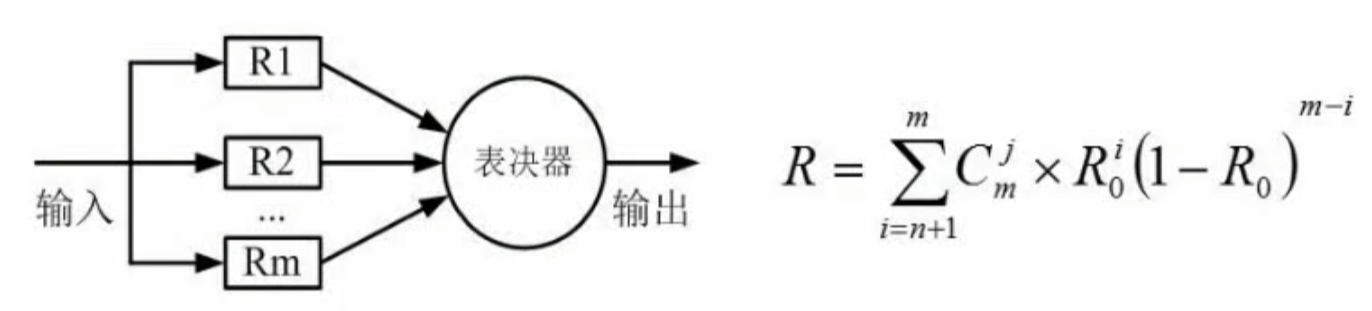
校验码
基本概念
检错和纠错的方法就是提高码距
码距:整个编码系统中任意(所有)两个码字的最小距离
- 在一个码组内为了检测e个误码,要求最小码距d应该满足:d>=e+1
- 在一个码组内为了纠正t个误码,要求最小码距d应该满足:d>=2t+1
若用1位长度的二进制编码,若A=1,B=0,这样A、B之间的最小码距为1
若用2位长度的二进制编码,若A=11,B=00,这样A、B之间的最小码距为1
若用3位长度的二进制编码,可选用111,000作为合法编码,A、B之间的最小码距为3
循环校验码CRC
考试中所认可的标准:可以做检错,不能做纠错
用到模2除法:做除法运算的过程中不计其进位的除法
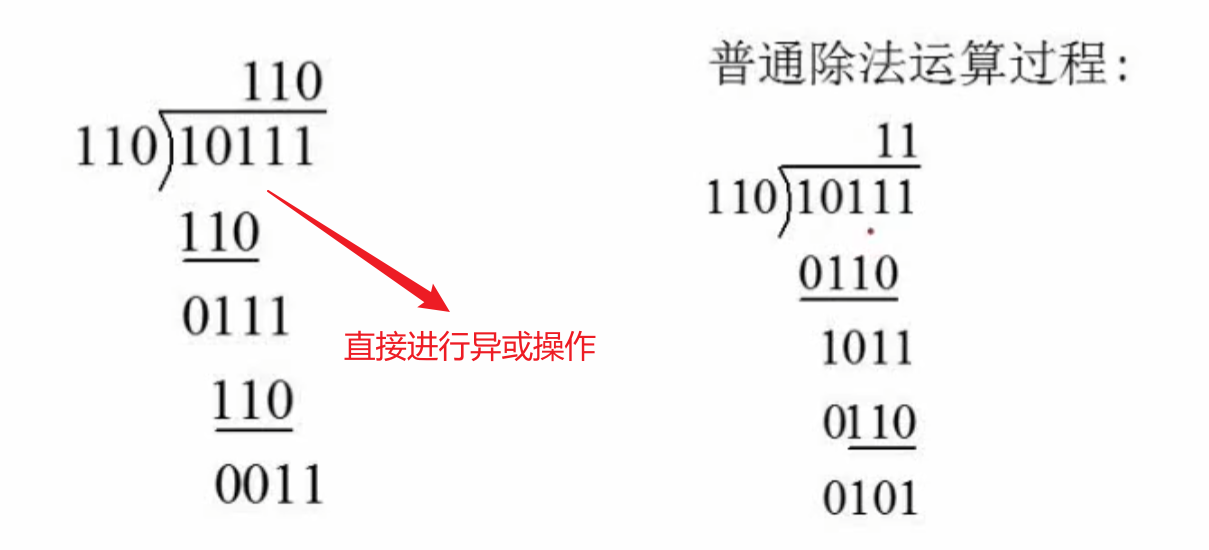
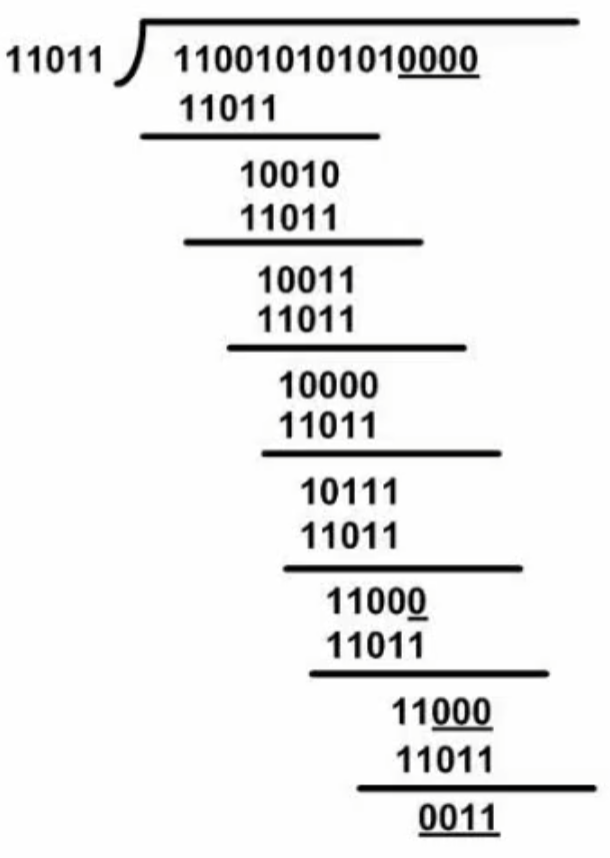
原始报文为
11001010101,其生成多项式为:,对其进行CRC编码:
- 生成多项式,对应二进制的位数为0还是1,本例中为11011
- 编码时,要对原始报文用0进行末尾补位,补位长度为生成多项式长度-1
- 最后进行模2除法,得到余数后,替换补位
- 收到编码信息后,将编码与生成多项式进行模2除法,得到的余数应该是0
海明校验码
难点,考查频度高
了解海明码编码基本规则,知道如何编码,计算多少位信息位需要多少个校验位
要求校验位的位置应为2n位
例,要放1个信息位,则长度应为3位,因为前两位都是校验码
假设校验码有r位,信息位有x位,则
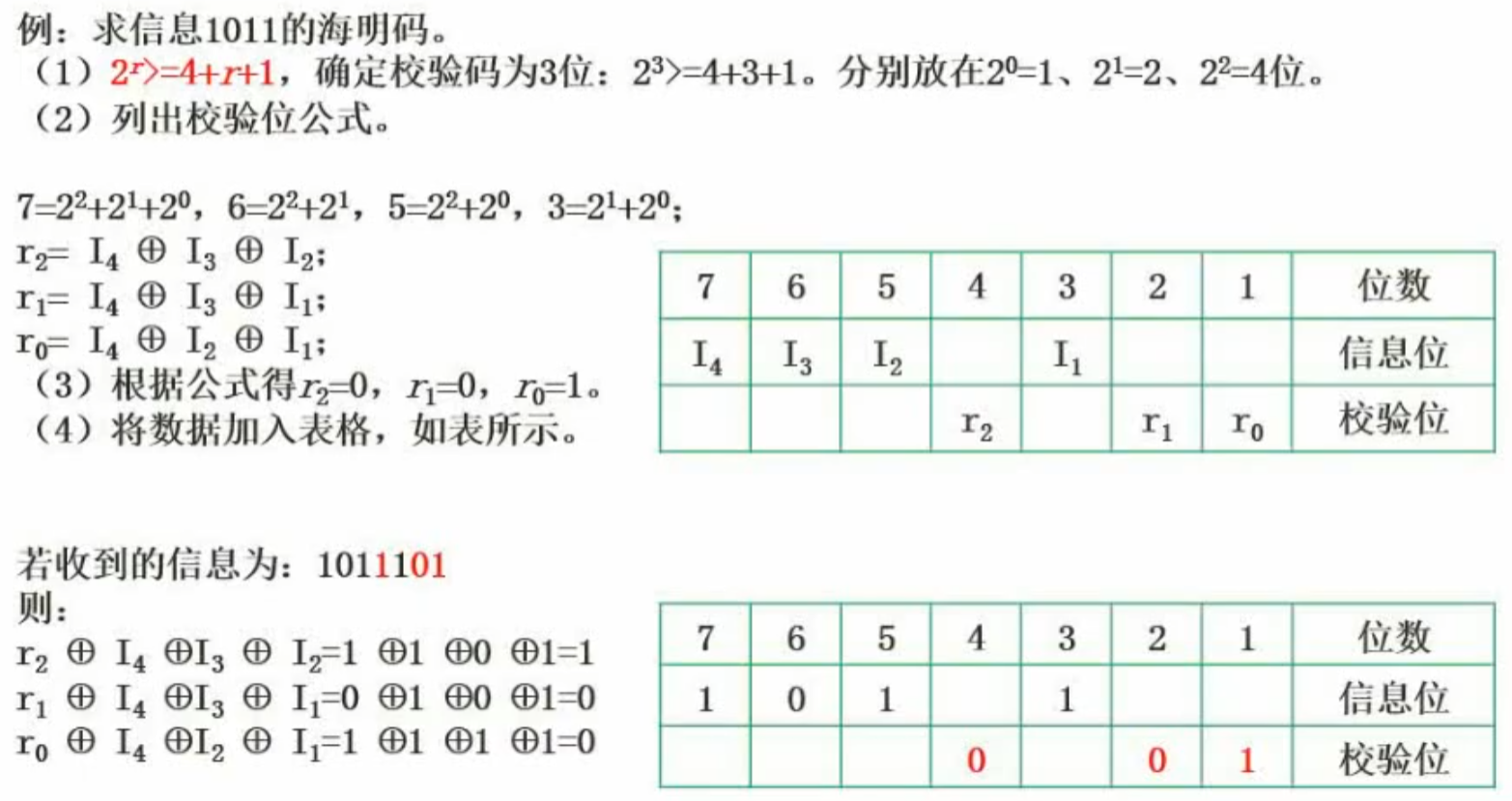
海明校验码可以检错,也可以纠错,若校验位不同,则可以根据出错的校验位定位到出错的信息位
本文作者:Morales
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 License 许可协议。转载请注明出处!