请注意,本文编写于 236 天前,最后修改于 236 天前,其中某些信息可能已经过时。
目录
分治法
对一个规模为n的问题,若该问题可以容易地解决(比如n较小)则直接解决;否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解决这些子问题,然后将各子问题的解合并得到原问题的解
- 该问题的规模缩小到一定的程度就可以容易地解决
- 该问题可以分解为若干个规模较小的相同问题
- 利用该问题分解出的子问题的解可以合并为该问题的解
- 该问题所分解出的各个子问题是相互独立的
分解、解决、合并
递归
在运行的过程中调用自己
c++// 斐波那契数列递归求解
int F(int n)
{
if(n == 0) return 1;
if(n == 1) return 1;
if(n > 1) return F(n - 1) + F(n - 2);
}

应用:二分查找
javascript/**
* L: 要查找的数列
* a, b: 要查找的区间范围起点和终点
* x: 要查找的值
*/
function Binary_Search(L, a, b, x) {
if (a > b) {
return (-1)
} else {
const m = (a + b) / 2;
if (x === L[m]) {
return m
} else if (x > L[m]) {
return Binary_Search(L, m + 1, b, x)
} else {
return Binary_Search(L, a, m - 1, x)
}
}
}
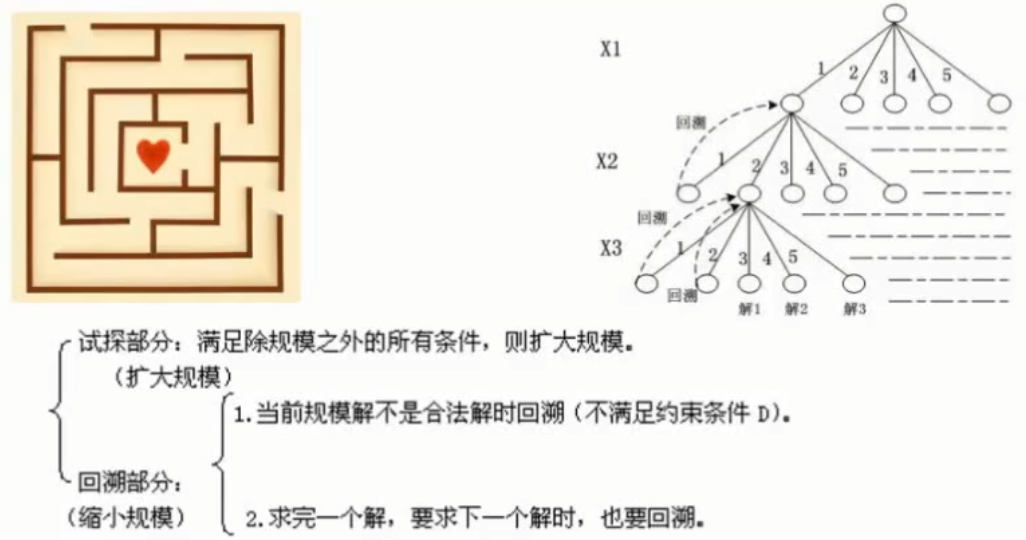
回溯法
是一种深度优先的搜索法,按选优条件向前搜索,以达到目标。但当搜索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。
适用于迷宫问题
贪心法
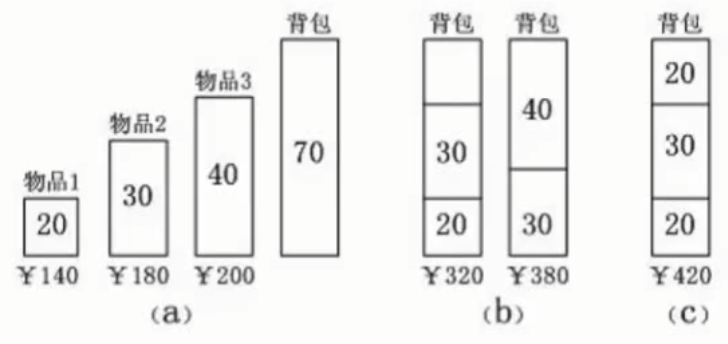
总是做出在当前来说是最好的选择,而并不从整体上加以考虑,它所做的每步选择只是当前步骤的局部最优选择,但从整体来说不一定是最优的选择
不必为了寻找最优解而穷尽所有可能解,耗费时间少,但得不到最优解
解决背包问题
动态规划法
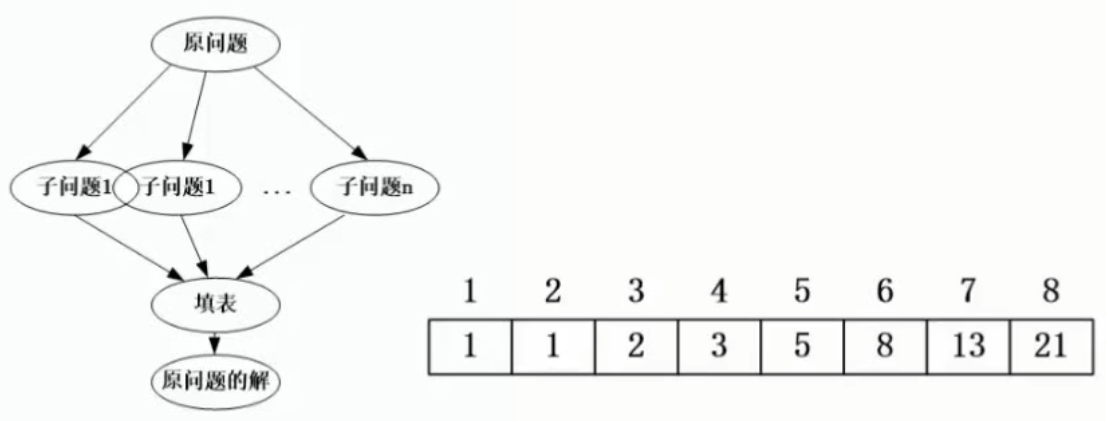
在求解问题中,对于每一步决策,列出各种可能的局部解,再依据某种判定条件,舍弃那些肯定不能得到最优解的局部解,在每一步都经过筛选,以每一步都是最优解来保证全局是最优解
动态规划一般要用到查表
推荐题目:力扣打家劫舍
案例分析
试题1





两种策略都不能确保得到最优解
试题2




本文作者:Morales
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 License 许可协议。转载请注明出处!
目录