Morales Blog
字符串匹配算法
2022-01-29
开发杂谈
0
请注意，本文编写于 1244 天前，最后修改于 517 天前，其中某些信息可能已经过时。

目录

BF算法
分析
代码实现
效率
RK算法
分析
代码实现
效率
KMP算法
分析
next数组
代码实现
效率
Sunday算法
分析
效率
相关题目

给定两个字符串A和B，请判断B是否是A的子串。 如果是，返回B在A中第一次出现的位置； 如果不是，返回-1。

什么意思呢？我们来举一个例子：

字符串A： a b b c e f g h 字符串B： b c e

字符串B是A的子串，B第一次在A中出现的位置下标是2，所以返回 2。

字符串A： a b c d e f g h 字符串B： a d e g

字符串B在A中并不存在，所以返回 -1。

为了统一概念，在后文中，我们把字符串A称为主串，把字符串B称为模式串。

BF算法

Brute Force（暴力算法）的缩写。

分析

直接从头开始，把主串和模式串的字符逐个进行匹配，如果发现不匹配，再从主串下一位开始，比较简单粗暴。

第一轮，从主串的第0位开始，把主串和模式串的字符逐个比较：

image.png

显然两者并不匹配。

第二轮，把模式串后移一位，从主串的第1位开始，把主串和模式串的字符逐个比较：

image.png

主串的第1位字符是b，模式串的第1位字符也是b，两者匹配，继续比较：

image.png

主串的第2位字符是b，模式串的第2位字符是c，两者并不匹配。

第三轮，把模式串再次后移一位，从主串的第2位开始，把主串和模式串的字符逐个比较：

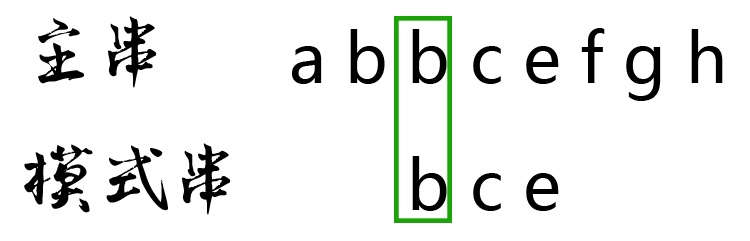
image.png

主串的第2位字符是b，模式串的第2位字符也是b，两者匹配，继续比较：

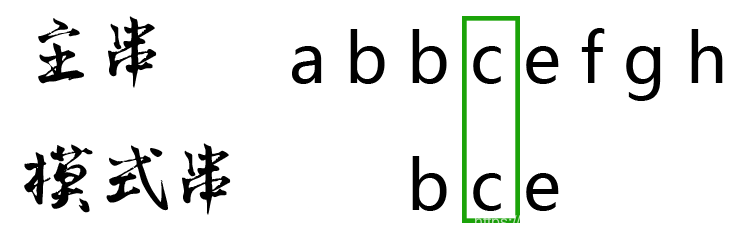
image.png

主串的第3位字符是c，模式串的第3位字符也是c，两者匹配，继续比较：

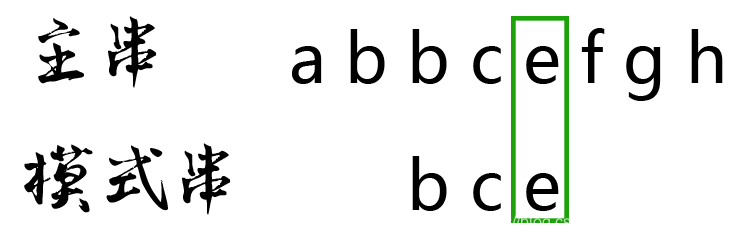
image.png

主串的第4位字符是e，模式串的第4位字符也是e，两者匹配，比较完成。

由此得到结果，模式串 bce 是主串 abbcefgh 的子串，在主串第一次出现的位置下标是 2：

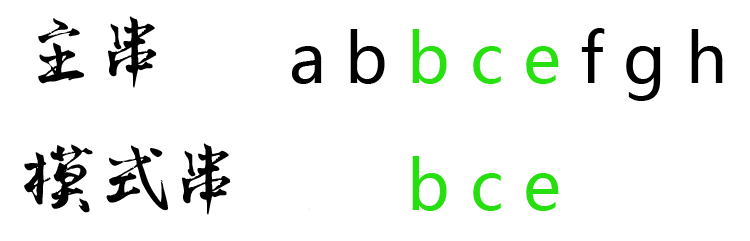
image.png

代码实现

c++
#include<bits/stdc++.h>
using namespace std;
int main()
{
    string s1 = "abbcefgh";
    string s2 = "bce";
    //cin>>s1>>s2;
    int n1=s1.size(), n2=s2.size();
    int i=0, j=0;
    int flag = 0;
    while(i<n1 && j<n2)
    {
        if(s1[i]==s2[j])
        {
            i++;
            j++;
        }
        else
        {
            i = i-j+1;
            j = 0;
        }
        if(j==n2)
        {
            cout<<i-n2<<endl;
            break;
        }
    }
    return 0;
}

效率

字符逐个比较，在某些极端情况下效率极低，例如：

主串： dddddddddddddn 模式串： dddn

假设主串的长度是m，模式串的长度是n，那么在这种极端情况下，BF算法的最坏时间复杂度是O(mn)。

RK算法

全称Rabin-Karp算法，以其发明者Rabin和Karp的名字命名。

分析

RK算法比较的是两个字符串的哈希值。

每一个字符串都可以通过某种哈希算法，转换成一个整型数，这个整型数就是hashcode：hashcode = hash(string)

显而易见，相对于逐个字符比较两个字符串，仅比较两个字符串的hashcode要容易得多。

第一步，需要生成模式串的hashcode。

生成hashcode的算法多种多样，比如：

  • 按位相加 这是最简单的方法，我们可以把a当做1，b当做2，c当做3......然后把字符串的所有字符相加，相加结果就是它的hashcode。 bce = 2 + 3 + 5 = 10 但是，这个算法虽然简单，却很可能产生hash冲突，比如bce、bec、cbe的hashcode是一样的。
  • 转换成26进制数 既然字符串只包含26个小写字母，那么我们可以把每一个字符串当成一个26进制数来计算。 bce = 2*(26^2) + 3*26 + 5 = 1435 这样做的好处是大幅减少了hash冲突，缺点是计算量较大，而且有可能出现超出整型范围的情况，需要对计算结果进行取模。

为了方便演示，此处采用按位相加的hash算法，所以bce的hashcode是10：

image.png

第二步，生成主串当中第一个等长子串的hashcode。

由于主串通常要长于模式串，把整个主串转化成hashcode是没有意义的，只有比较主串当中和模式串等长的子串才有意义。

因此，我们首先生成主串中第一个和模式串等长的子串hashcode，即abb = 1 + 2 + 2 = 5：

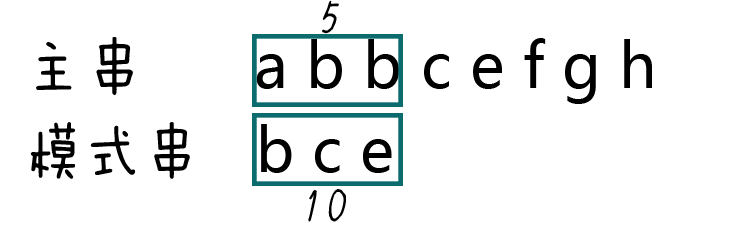image.png 第三步，比较两个hashcode。

显然5 != 10，说明模式串和第一个子串不匹配，继续下一轮比较。

第四步，生成主串当中第二个等长子串的hashcode。

bbc = 2 + 2 + 3 = 7：

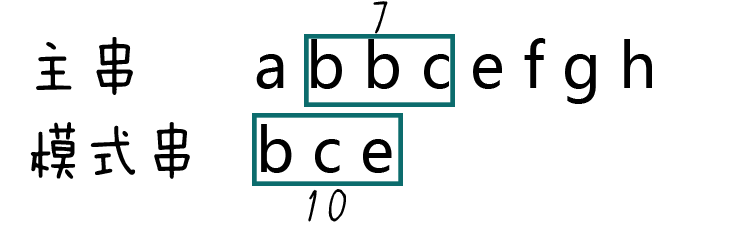
image.png

第五步，比较两个hashcode。

显然7!=10，说明模式串和第二个子串不匹配，继续下一轮比较。

第六步，生成主串当中第三个等长子串的hashcode。

bce= 2 + 3 + 5 = 10：

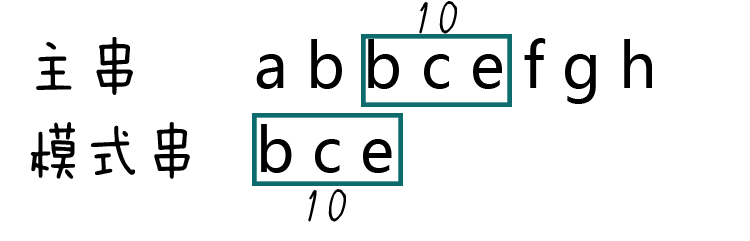
image.png

第七步，比较两个hashcode。

显然10==10，两个hashcode相等。

第八步，逐个字符比较两字符串。

hashcode的比较只是初步验证，之后我们还需要像BF算法那样，对两个字符串逐个字符比较，最终判断出两个字符串匹配。

最后得出结论，模式串bce是主串abbcefgh的子串，第一次出现的下标是2：

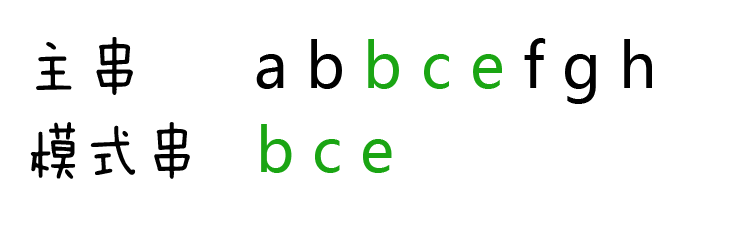
image.png

代码实现

c++
#include<bits/stdc++.h>
using namespace std;
int Hash(string str) // 计算hashcode 
{
    int hashcode = 0;
    for(int i=0; i<str.size(); i++)
        hashcode += str[i]-'a'; // 以按位相加方法 
    return hashcode;
}
bool comp(int index, string s1, string s2) // 进行精确比较
{
    if(s1.compare(index, s2.size(), s2) == 0) return 1;
    //if(s1.substr(index, s2.size()) == s2) return 1;  皆可
    else return 0; 
}
int RK(string str1, string str2)
{
    int n1=str1.size(), n2=str2.size();
    int code1 = Hash(str1.substr(0, n2));
    int code2 = Hash(str2);
    for(int i=0; i<n1-n2+1; i++)
    {
        //cout<<code1<<" "<<code2<<endl;
        if(code1==code2 && comp(i, str1, str2)) return i;
        // 判断是否已进行到最后一轮 
        if(i < n1-n2) // 若非最后一轮
        {
            code1 -= str1[i]-'a';
            code1 += str1[i+n2]-'a';
        } // 更新hash值
    }
    return -1; // 若非子串则返回-1
}
int main()
{
    string s1 = "abbcefgh";
    string s2 = "bce";
    cout<<RK(s1, s2)<<endl; // 输出第一次出现的下标 
    return 0;
}

效率

RK算法计算单个字串hash的时间复杂度是O(n)，且由于后续字串的hash为增量计算，时间复杂度仍为O(n)。

RK算法的缺点在于哈希冲突，每次冲突产生时，RK算法都要对子串和模式串进行逐个字符比较，当冲突过多时，RK算法就退化为BF算法了。

KMP算法

全称Knuth-Morris-Pratt算法，由D.E.Knuth，J.H.Morris，V.R.Pratt研究而得。又名“看猫片”算法。

分析

假设现在主串A匹配到 i 位置，模式串B匹配到 j 位置：

  • 如果j == -1，或者当前字符匹配成功（即A[i] == B[j]），则令i++，j++，继续匹配下一个字符；
  • 如果j != -1，且当前字符匹配失败（即A[i] != B[j]），则令 i 不变，j = next[j]。这种操作意味着失配（不匹配）时，模式串相对于主串向右移动了j - next [j] 位。

当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值，即 移动的实际位数为：j - next[j]，且此值大于等于1。

第一步，主串逐位与模式串第0位比较，直至二者匹配。

a与b不匹配，j=0，i++，此时b与b匹配。

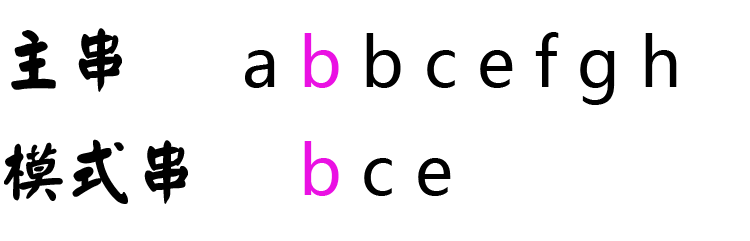
image.png

第二步，两串指针均后移一位，进行比较。

i++，j++，此时j=1，且b与c不匹配。

image.png

当模式串中j 处的字符失配时，下一步用next[j]处的字符继续跟主串匹配，相当于模式串向右移动j - next[j] 位。

第三步，i不变，j回溯。

模式串相对于主串移动了j-next[j]位。

image.png

此时b==b，匹配。

第四步，两串指针均后移一位，进行比较。

匹配完成。

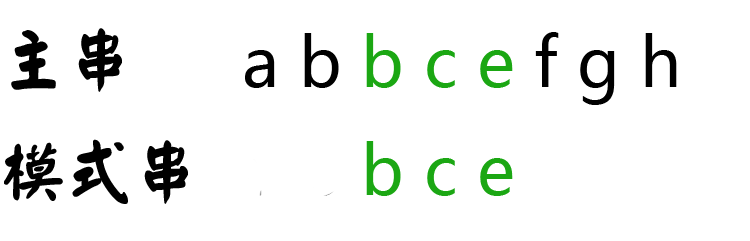
image.png

阮一峰的思路讲解

next数组

next数组与“部分匹配表”（储存“部分匹配值”的表）有关。“部分匹配值”是"前缀"和"后缀"的最长的共有元素的长度。

  • "前缀"：除了最后一个字符以外，一个字符串的全部头部组合；
  • "后缀"：除了第一个字符以外，一个字符串的全部尾部组合。

以字符串ABCDABD为例：

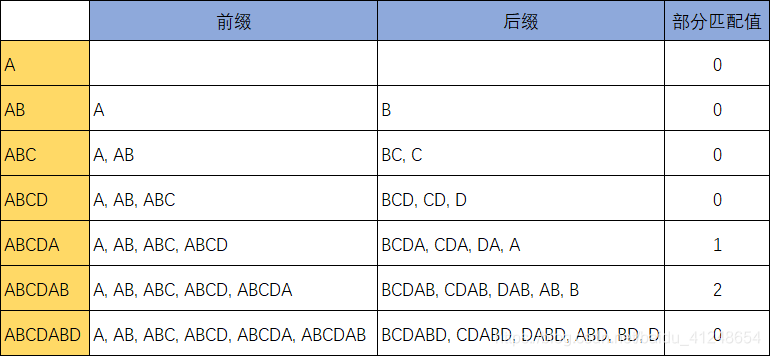
image.png

据此表可得结论：失配时，模式串向右移动的位数 = 已匹配字符数 - 失配字符的上一位字符所对应的部分匹配值。

当匹配到一个字符失配时，我们看到的是失配字符的上一位字符对应的部分匹配值。如此，便有next 数组：

ABCDABD
部分匹配值0000120
next数组值-1000012

据此next数组，得到：失配时，模式串向右移动的位数 = 失配字符所在位置 - 失配字符对应的next 值。

计算next 数组可以采用递推的方法。

对于P的前j+1个序列字符：

  • 若p[k] == p[j]，则next[j + 1 ] = next [j] + 1 = k + 1；
  • 若p[k] ≠ p[j]，如果此时p[ next[k] ] == p[j ]，则next[ j + 1 ] = next[k] + 1，否则继续递归前缀索引k = next[k]，而后重复此过程。 相当于在字符p[j+1]之前不存在长度为k+1的前缀"p0 p1, …, pk-1 pk"跟后缀"pj-k pj-k+1, …, pj-1 pj"相等，那么是否可能存在另一个值t+1 < k+1，使得长度更小的前缀 “p0 p1, …, pt-1 pt” 等于长度更小的后缀 “pj-t pj-t+1, …, pj-1 pj” 呢？如果存在，那么这个t+1 便是next[ j+1]的值，此相当于利用已经求得的next 数组（next [0, ..., k, ..., j]）进行P串前缀跟P串后缀的匹配。

详细计算方法参考

代码实现

c++
#include<bits/stdc++.h>
using namespace std;
int Next[10];
void getNEXT(string str)
{
    Next[0] = -1;
    int i=-1, j=0;
    while(j < str.size()-1)
    { // str[i]表示前缀，str[j]表示后缀 
        if(i==-1 || str[j]==str[i])
        {
            i++;
            j++;
            Next[j] = i;
            if(str[j] != str[i]) Next[j] = i;
            else Next[j] = Next[i];
        }
        else i = Next[i];
    }
}
int KMP(string str1, string str2)
{
    int i=0, j=0; // 两串的指针
    int len1=str1.size(), len2=str2.size();
    while(i<len1 && j<len2)
    {
        if(j==-1 || str1[i]==str2[j])
        {
            i++;
            j++;
        }
        else j = Next[j];
    }
    if(j == len2)
        return i-j;
    else return -1;
}
int main()
{
    string s1 = "abbcefgh";
    string s2 = "bce";
    getNEXT(s2);
    cout<<KMP(s1, s2)<<endl;
    return 0;
}
  1. 匹配失败时，总是能够让 pattern 回退到某个位置，使 text 不用回退。
  2. 在字符串比较时，pattern 提供的信息越多，计算复杂度越低。

效率

如果某个字符匹配成功，模式串首字符的位置保持不动，仅仅是i++、j++；如果匹配失配，i 不变（即 i 不回溯），模式串会跳过匹配过的next [j]个字符。整个算法最坏的情况是，当模式串首字符位于i - j的位置时才匹配成功，算法结束。

所以，如果主串的长度为n，模式串的长度为m，那么匹配过程的时间复杂度为O(n)，算上计算next的O(m)时间，KMP的整体时间复杂度稳定在O(m + n)。

Sunday算法

是Daniel M.Sunday于1990年提出的一种字符串模式匹配算法。

分析

Sunday算法的核心思想是：在匹配过程中，模式串并不被要求一定要按从左向右进行比较还是从右向左进行比较，它在发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配。

我们对模式串做一个简单而巧妙的预处理：记录模式串中每一种字符最后出现的位置，将其存入一个数组中。

bce
012

我们假定主串名为str，长度为n；模式串名为pattern，长度为m。

若在发生不匹配时str[i]≠pattern[j]，0≤i<n，0≤j<n。设str此次第一个匹配的字符位置为L。显然，str[L+m]肯定要参加下一轮的匹配，并且pattern至少要与str[L+m]匹配才有可能与整个str匹配。

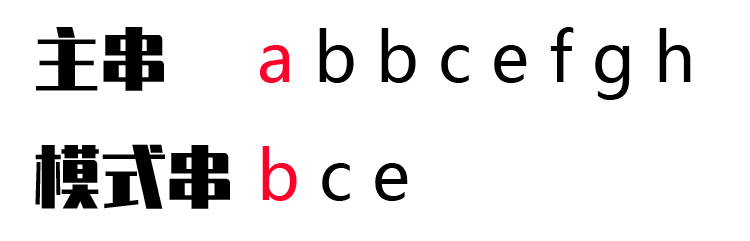
此时不匹配，i=0，j=0，L=1

这时就可以寻找pattern中str[L+m]出现的位置了。利用我们预处理好的数组，可以O(1)查找出该位置K，并将其直接移动至pattern[K]==str[L+m]。特殊地，若str[L+m]没有在pattern中出现，那么pattern不可能会与str[L+m]匹配，则将pattern的第一位直接移动到str[L+m+1]，继续匹配。直至L+m > n时，匹配完毕。

str[L+m]=='e'，pattern[K]=='e'

c++
#include<bits/stdc++.h>
using namespace std;
int Lpos[256]; // 记录模式串中每一种字符最后出现的位置
int str, pattern;
void mem(string s)
{
    memset(Lpos, -1, sizeof(Lpos));
    for(int i=0; i<=pattern; i++)
        Lpos[s[i]] = i;
}
int Sunday(string str1, string str2)
{
    int L=0;
    while(L+pattern <= str)
    {
        int i=0;
        bool flag=1;
        while(i<=pattern && flag)
        {
            if(str1[L+i] != str2[i]) flag=0;
            i++;
        }
        if(flag)
            return L;
        else
        {
            i = pattern+1;
            if(Lpos[str1[L+i]] == -1) L += i+1;
            else L += i-Lpos[str1[L+i]];
        }
    }
    return -1;
}
int main()
{
    string s1 = "abbcefgh";
    string s2 = "bce";
    str = s1.size()-1;
    pattern = s2.size()-1;
    mem(s2);
    cout<<Sunday(s1, s2)<<endl;
    return 0;
}

效率

平均性能的时间复杂度为O(n)，最差情况的时间复杂度为O(nm)。

Sunday算法的扫描顺序是没有限制的。为了提高在最坏情况下的算法效率，可以对模式串中的字符按照其出现的概率从小到大的顺序扫描，这样能尽早地确定失配与否。

相关题目

NEFU OJ：

HDU：

本文作者:Morales

本文链接:

版权声明:本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 License 许可协议。转载请注明出处！